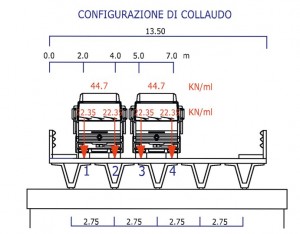
 Nell’ambito dei ponti di luce corrente ricorre sovente l’impiego di travi a sezione scatolare ottenute solidarizzando in opera travi precompresse a profilo aperto con una soletta collaborante che unisce tra loro all’estradosso le travi dell’impalcato. Come per le altre tipologie, anche per gli impalcati composti da travi a sezione chiusa si presenta la necessità sia in sede di progetto che di collaudo di individuare la ripartizione dei carichi mobili. Per tale analisi i codici automatici oggi a disposizione consentono di effettuare una modellazione anche sofisticata dello schema strutturale, tuttavia permane non meno attuale la necessità di disporre di strumenti che permettono di operare sintesi fondamentali sia in sede di dimensionamento che di verifica. A questo riguardo i modelli di analogia al continuo costituiscono ancora oggi uno strumento affidabile come la consolidata applicazione del modello di Bares-Massonet [1] ha largamente dimostrato nei suoi molti anni di utilizzo, al punto tale che il modello a piastra ortotropa è tuttora largamente impiegato nella stesura dei progetti esecutivi da parte di molte ditte produttrici di travi precompresse. Va peraltro ricordato come tale modello sia nato in realtà per impalcati di travi aventi sezioni con modesta rigidezza torsionale, ossia per valori limiti del parametro di torsione riconducili da un lato ad impalcati privi di rigidezza torsionale (a=0) e dall’altro lato a solette piene (a=1). In precedenti contributi è già stata mostrata la possibilità di estendere nel modello a piastra ortotropa l’interpolazione utilizzata nel metodo di Bares-Massonet anche agli impalcati dotati di elevata rigidezza torsionale (a>1) mantenendo in tal modo un approccio unitario nello studio della ripartizione dei carichi (Lenzi [2]). In tale ottica la presente nota completa l’analisi sfruttando la proprietà degli impalcati composti da travi a sezione chiusa con soletta collaborante di essere contraddistinti da una marcata differenza tra la rigidezza flesso torsionale delle travi in direzione longitudinale e la rigidezza della soletta in direzione trasversale essendo in genere assenti in questi impalcati, con qualche eccezione limitata all’ambito ferroviario, i traversi in campata. La superficie elastica viene ancora ricercata in forma analitica spalmando al continuo le rigidezze flesso torsionali delle travi sul loro interasse. Nel caso in esame tuttavia l’analisi si semplifica notevolmente potendosi trascurare per le ipotesi assunte i termini relativi alle rigidezze trasversali della soletta, che risulta sollecitata solo dai tagli mu – tui trasversali che si scambiano le travi e che operano la ripartizione. Si ricava in tal modo una soluzione di semplice utilizzo che si dimostra essere, tramite il confronto con altri metodi numerici e con le misure in sito, di piena validità nell’ambito s’intende delle ipotesi assunte. Il modello al continuo ha poi il pregio di fornire una soluzione in for – ma chiusa parametrica e adimensionale che presenta molteplici vantaggi riconducibili ai seguenti aspetti operativi: 1) individuazione del numero minimo di parametri necessari per la definizione del problema.
Nell’ambito dei ponti di luce corrente ricorre sovente l’impiego di travi a sezione scatolare ottenute solidarizzando in opera travi precompresse a profilo aperto con una soletta collaborante che unisce tra loro all’estradosso le travi dell’impalcato. Come per le altre tipologie, anche per gli impalcati composti da travi a sezione chiusa si presenta la necessità sia in sede di progetto che di collaudo di individuare la ripartizione dei carichi mobili. Per tale analisi i codici automatici oggi a disposizione consentono di effettuare una modellazione anche sofisticata dello schema strutturale, tuttavia permane non meno attuale la necessità di disporre di strumenti che permettono di operare sintesi fondamentali sia in sede di dimensionamento che di verifica. A questo riguardo i modelli di analogia al continuo costituiscono ancora oggi uno strumento affidabile come la consolidata applicazione del modello di Bares-Massonet [1] ha largamente dimostrato nei suoi molti anni di utilizzo, al punto tale che il modello a piastra ortotropa è tuttora largamente impiegato nella stesura dei progetti esecutivi da parte di molte ditte produttrici di travi precompresse. Va peraltro ricordato come tale modello sia nato in realtà per impalcati di travi aventi sezioni con modesta rigidezza torsionale, ossia per valori limiti del parametro di torsione riconducili da un lato ad impalcati privi di rigidezza torsionale (a=0) e dall’altro lato a solette piene (a=1). In precedenti contributi è già stata mostrata la possibilità di estendere nel modello a piastra ortotropa l’interpolazione utilizzata nel metodo di Bares-Massonet anche agli impalcati dotati di elevata rigidezza torsionale (a>1) mantenendo in tal modo un approccio unitario nello studio della ripartizione dei carichi (Lenzi [2]). In tale ottica la presente nota completa l’analisi sfruttando la proprietà degli impalcati composti da travi a sezione chiusa con soletta collaborante di essere contraddistinti da una marcata differenza tra la rigidezza flesso torsionale delle travi in direzione longitudinale e la rigidezza della soletta in direzione trasversale essendo in genere assenti in questi impalcati, con qualche eccezione limitata all’ambito ferroviario, i traversi in campata. La superficie elastica viene ancora ricercata in forma analitica spalmando al continuo le rigidezze flesso torsionali delle travi sul loro interasse. Nel caso in esame tuttavia l’analisi si semplifica notevolmente potendosi trascurare per le ipotesi assunte i termini relativi alle rigidezze trasversali della soletta, che risulta sollecitata solo dai tagli mu – tui trasversali che si scambiano le travi e che operano la ripartizione. Si ricava in tal modo una soluzione di semplice utilizzo che si dimostra essere, tramite il confronto con altri metodi numerici e con le misure in sito, di piena validità nell’ambito s’intende delle ipotesi assunte. Il modello al continuo ha poi il pregio di fornire una soluzione in for – ma chiusa parametrica e adimensionale che presenta molteplici vantaggi riconducibili ai seguenti aspetti operativi: 1) individuazione del numero minimo di parametri necessari per la definizione del problema.
[pdf http://www.prog-res.it/frames/wp-content/uploads/2010/08/20101012_un_modello_al_continuo_per_lo_studio_degli_impalcati_di_travi_scatolari.pdf]